Fórmula para calcular YTM
La fórmula de rendimiento al vencimiento se refiere a la fórmula que se utiliza para calcular el rendimiento total que se anticipa sobre el bono en caso de que el mismo se mantenga hasta su vencimiento y, según la fórmula, el rendimiento al vencimiento se calcula restando el valor presente de la seguridad de valor nominal del valor, divídalos por el número de años de vencimiento y súmelos con el pago del cupón y luego dividiendo el resultado con la suma del valor presente del valor y el valor nominal del valor dividido por 2.

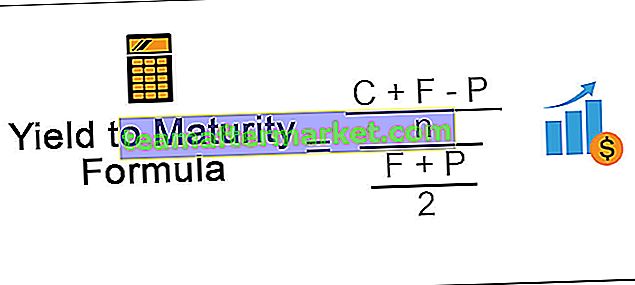
Dónde,
- C es el Cupón.
- F es el valor nominal del bono.
- P es el precio de mercado actual.
- n serán los años hasta el vencimiento.
Cálculo paso a paso del rendimiento al vencimiento (YTM)
- Paso 1: Recopiló la información sobre el valor nominal del bono, los meses que faltan para el vencimiento, el precio de mercado actual del bono, la tasa de cupón del bono.
- Paso 2: Ahora calcule el ingreso anual disponible en el bono, que es principalmente el cupón y podría pagarse anualmente, semestralmente, trimestralmente, mensualmente, etc. y, en consecuencia, se debe realizar el cálculo.
- Paso 3: Además, es necesario amortizar el descuento o la prima que es una diferencia entre el valor nominal del bono y el precio actual de mercado durante la vida del bono.
- Paso 4: El numerador de la fórmula YTM será la suma de la cantidad calculada en el paso 2 y el paso 3.
- Paso 5: El denominador de la fórmula YTM será el promedio del precio y el valor nominal.
- Paso 6: Cuando se divide el valor del paso 4 por el paso 5, será el rendimiento aproximado al vencimiento.
Ejemplos
Puede descargar esta plantilla de Excel de fórmula de rendimiento al vencimiento (YTM) aquí - Plantilla de Excel de fórmula de rendimiento al vencimiento (YTM)Ejemplo 1
Suponga que el precio del bono es $ 940 con el valor nominal del bono de $ 1000. La tasa de cupón anual es del 8% con un vencimiento de 12 años. Con base en esta información, debe calcular el rendimiento aproximado al vencimiento.
Solución:
Utilice los datos que se proporcionan a continuación para calcular el rendimiento al vencimiento.

Podemos utilizar la fórmula anterior para calcular el rendimiento aproximado al vencimiento.
El cupón del bono será de $ 1,000 * 8%, que es de $ 80.
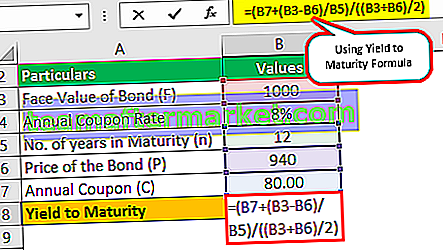
Rendimiento hasta el vencimiento (aprox.) = (80 + (1000 - 94) / 12) / ((1000 + 940) / 2)
El rendimiento hasta el vencimiento será:
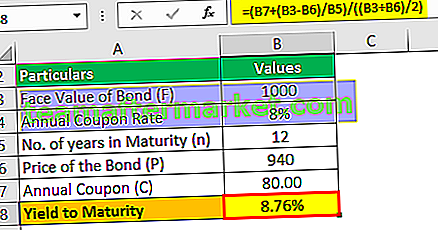
Rendimiento al vencimiento (aprox.) = 8,76%
Se trata de un rendimiento aproximado al vencimiento que será del 8,76%.
Ejemplo # 2
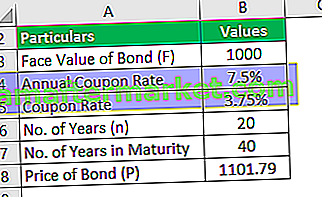
FANNIE MAE es una de las marcas famosas que cotizan en el mercado estadounidense. El gobierno de los Estados Unidos ahora quiere emitir un bono fijo de pago semestral a 20 años para su proyecto. El precio del bono es $ 1,101.79 y el valor nominal del bono es $ 1,000. La tasa de cupón es del 7.5% sobre el bono. Con base en esta información, debe calcular el rendimiento aproximado al vencimiento del bono.
Solución:
Utilice los datos que se proporcionan a continuación para calcular el rendimiento al vencimiento.
El cupón del bono será de $ 1,000 * 7.5% / 2 que es $ 37.50, ya que se paga semestralmente.
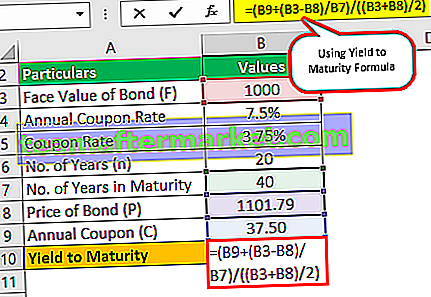
Rendimiento al vencimiento (aprox.) = (37,50 + (1000 - 1101,79) / (20 * 2)) / ((1000 + 1101,79) / 2)
El rendimiento hasta el vencimiento será:
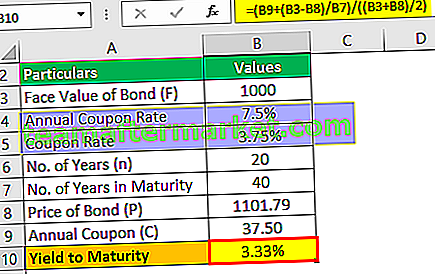
Rendimiento al vencimiento (aprox.) = 3,33%
Se trata de un rendimiento aproximado al vencimiento que será del 3,33% semestral.
El rendimiento anual hasta el vencimiento será:
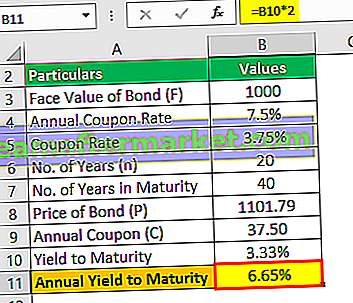
Por lo tanto, el rendimiento anual al vencimiento será del 3,33% * 2, que será del 6,65%.
Ejemplo # 3
El Sr. Rollins ha recibido la suma global en forma de lotería. Es una persona reacia al riesgo y cree en el bajo riesgo y la alta rentabilidad. Se acerca al asesor financiero y el asesor le dice que él es el mito equivocado de bajo riesgo y alta rentabilidad. Entonces, el Sr. Rollins acepta que no le gustan los riesgos y que la inversión de bajo riesgo con un rendimiento bajo es suficiente. El asesor le da dos opciones de inversión y los detalles de ellas se encuentran a continuación:

Ambos cupones se pagan semestralmente. Ahora el Sr. Rollins está perplejo sobre qué vínculo elegir. Le pide a Advisor que invierta en la opción 2 ya que el precio del bono es menor y está dispuesto a sacrificar un cupón del 0,50%. Sin embargo, Advisor le dice que, en cambio, invierta en la opción 1.
Debe validar los consejos realizados por el asesor.
Solución:
Opción 1
El cupón del bono será de $ 1,000 * 9% / 2, que es de $ 45, ya que se paga semestralmente.
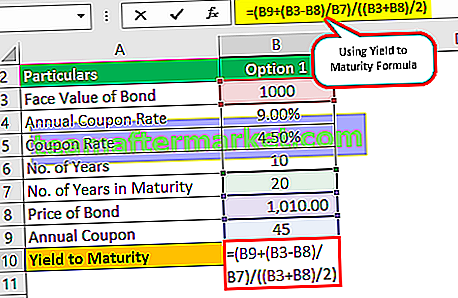
Rendimiento hasta el vencimiento (aprox.) = (45 + (1000 - 1010) / (10 * 2)) / ((1000 +1010) / 2)
El rendimiento hasta el vencimiento será:
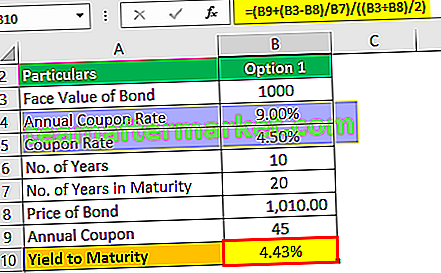
Rendimiento al vencimiento (aprox.) = 4,43%
Se trata de un rendimiento aproximado al vencimiento que será del 4,43% que es semestral.
El rendimiento anual hasta el vencimiento será:
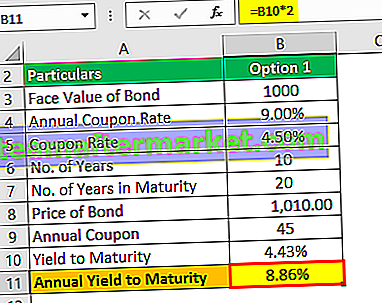
Por lo tanto, el rendimiento anual al vencimiento será del 4,43% * 2, que será del 8,86%.
opcion 2
El cupón del bono será de $ 1,000 * 8.50% / 2 que es $ 42.5, ya que se paga semestralmente.
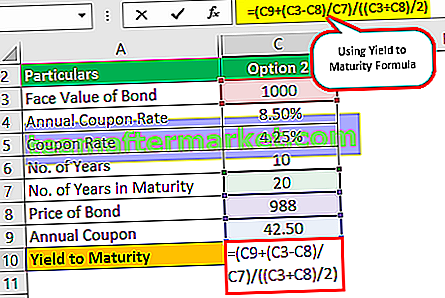
Rendimiento hasta el vencimiento (aprox.) = (42,50 + (1000 - 988) / (10 * 2)) / ((1000 +988) / 2)
El rendimiento hasta el vencimiento será:
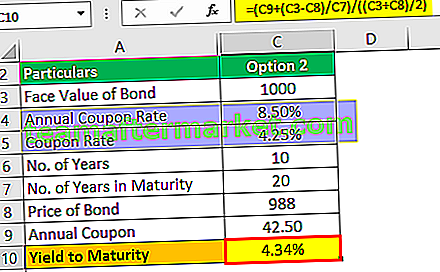
Rendimiento al vencimiento (aprox.) = 4,34%
Se trata de un rendimiento aproximado al vencimiento que será del 4,34%, que es semestral.
El rendimiento anual hasta el vencimiento será:
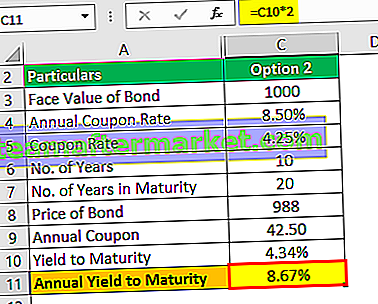
Por tanto, el rendimiento anual al vencimiento será del 4,34% * 2 que será del 8,67%.
Dado que el rendimiento al vencimiento es mayor en la opción 2, el asesor tiene razón al recomendar invertir en la opción 2 para el Sr. Rollins.
Relevancia y usos
La fórmula de rendimiento aproximado al vencimiento es casi similar al rendimiento actual que divide los flujos de efectivo que son cupones y amortiza las primas o descuentos por el precio del bono para determinar cuál es el rendimiento del bono si el inversor mantiene el bono durante un año. . Bueno, solo se aproxima el rendimiento al vencimiento y si se necesita calcular el rendimiento al vencimiento con precisión, entonces se necesita encontrar la TIR o la tasa a la que el cupón y los valores de amortización junto con el valor nominal que equivale al precio actual del mercado de bonos que puede hecho usando el método de prueba y error.